কোর্স:পাসপ্র/সমস্যা ৩.৪.১
সমস্যা
পূর্বে আমরা অজানা রাশির সাপেক্ষে রৈখিক অপেক্ষকের জন্য ন্যূনতম বর্গ নিরূপণের সমস্যা সমাধান করেছি। এখন দৃষ্টি নিক্ষেপ করব অরৈখিক অপেক্ষকের জন্য সর্বোচ্চ সম্ভাবনা ও ন্যূনতম বর্গ নিরূপণের দিকে। ধরি আমাদের উপাত্তটি এমন:
- <math>x[n] = r^n + w[n]</math>
যেখানে <math>n=0,1,2,...,N-1</math> এবং <math>w[n] \sim \mathcal{N}(0,\sigma^2)</math>
- অজানা রাশি r এর সর্বোচ্চ সম্ভাব্যতা নিরূপকের (সসনি) গাণিতিক রূপটি নির্ণয় করো। এই সমীকরণটি কি হাতে-কলমে সমাধান করা সম্ভব?
- নিউটন-রাফসন পদ্ধতি ব্যবহার করে প্রাপ্ত সসনি সমীকরণ টি'র একটি পৌনরুক্তিক (iterative) সমাধান নির্ণয় করো।
- উপর্যুক্ত পদ্ধতিটি একটি কম্পিউটার সিম্যুলেশনের মাধ্যমে প্রয়োগ করতে হবে। প্রথমে <math>N=50, \sigma^2=0.01, r=0.5</math> ধরে নিয়ে উপাত্তটি প্লট করো। তারপর r এর সাপেক্ষে <math>-\sum\limits_{n=0}^{N-1} (x[n]-r^n)^2</math> প্লট করো। <math>r=0.5</math> অঞ্চলটিতে জুম করো; অপেক্ষকটির সর্বোচ্চ মান কি ০.৫ এ? যদি হয়, তাহলে কেন?
- তারপর পৌনরুক্তিক উপায়ে <math>r</math> এর মান নিরূপণের জন্য একটি কম্পিউটার প্রোগ্রাম লিখো। প্রোগ্রামটি তিনটি পূর্বানুমিত আদিমানের (<math>r_0=[0.8, 0.2, 1.2]</math>) জন্য রান করো। প্রোগ্রামের মাধ্যমে নিরূপিত মানগুলোকে পুনরুক্তি সংখ্যার (১ থেকে ৩০) সাপেক্ষে প্লট করো। ফলাফল ব্যাখ্যা করো।
- এবার আদিমান ১.৪ ধরে প্রোগ্রামটি আবার রান করে দেখ কী ঘটে। ফলাফল ব্যাখ্যা করো।
সমাধান ১
সমাধান ২
সমাধান ৩
ম্যাটল্যাব প্রোগ্রামের মাধ্যমে প্রাপ্ত প্লটটি নিচে দেখানো হল। ডায়াগ্রামটিতে ক্লিক করে যে পাতায় যাওয়া যাবে সেখানে ডায়াগ্রামটির নিচে ম্যাটল্যাব কোডটুকুও দেয়া আছে।
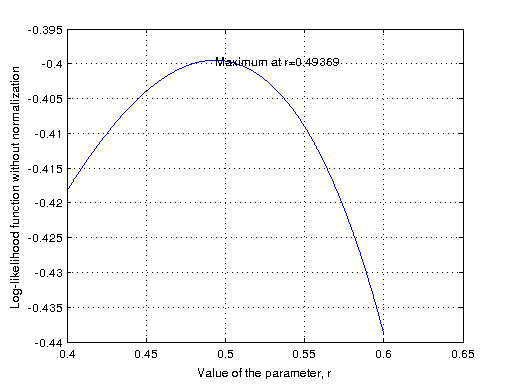
দেখা যাচ্ছে r এর মান ০.৪৯ এ লগ-সম্ভাব্যতা অপেক্ষকের সর্বোচ্চ মান পাওয়া যায়, যা আমাদের প্রকৃত মানের (r=০.৫) চেয়ে বেশ আলাদা। এর কারণ, সসনি কেবল রৈখিক মডেলের জন্যই নিটাল, আর আমাদের মডেলটি মোটেই রৈখিক নয়। অরৈখিক মডেলের জন্যও অসীম সংখ্যক উপাত্তের জন্য সসনি নিটাল হয়, কিন্তু আমরা উপাত্ত নিয়েছি মাত্র ৫০টি।
সমাধান ৪+৫
ম্যাটল্যাব প্রোগ্রামের মাধ্যমে প্রাপ্ত প্লটটি নিচে দেখানো হল। ডায়াগ্রামটিতে ক্লিক করে যে পাতায় যাওয়া যাবে সেখানে ডায়াগ্রামটির নিচে ম্যাটল্যাব কোডটুকুও দেয়া আছে।

সসনি সমীকরণটি হাতে-কলমে সমাধান করা যেতো না। এজন্য আমরা একটি কম্পিউটার প্রোগ্রামের মাধ্যমে নিউটন-রাফসন পদ্ধতি প্রয়োগ করে r এর মান নির্ণয় করেছি। এজন্য আমাদেরকে প্রথমে r এর একটি আদিমান অনুমান করে নিতে হয়েছে। এই পূর্বানুমিত মান প্রকৃত মানের কাছাকাছি, নিরূপিত মান প্রকৃত মানে পৌঁছাতে তত কম পুনরুক্তির দরকার পরে। দেখা যাচ্ছে পূর্বানুমিত মান ১.৪ হলে (যা r=০.৫ এর চেয়ে অনেক বেশি) নিরূপিত মান প্রকৃত মানের কাছাকাছি পৌঁছাতে ৪০ টিরও বেশি পুনরুক্তির দরকার পরে।